“Intel introduced the 8087 chip in 1980 to improve floating-point performance on the 8086 and 8088 processors, and it was used with the original IBM PC. Since early microprocessors operated only on integers, arithmetic with floating-point numbers was slow and transcendental operations such as arctangent or logarithms were even worse. Adding the 8087 co-processor chip to a system made floating-point operations up to 100 times faster.
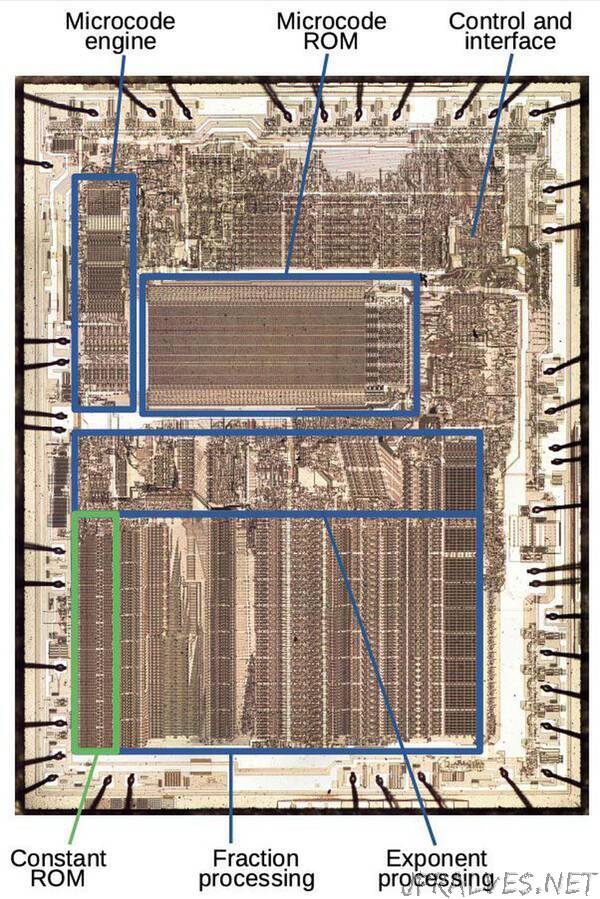
I opened up an 8087 chip and took photos with a microscope. The photo below shows the chip’s tiny silicon die. Around the edges of the chip, tiny bond wires connect the chip to the 40 external pins. The labels show the main functional blocks, based on my reverse engineering. By examining the chip closely, various constants can be read out of the chip’s ROM, numbers such as pi that the chip uses in its calculations.
The top half of the chip contains the control circuitry. Performing a floating-point instruction might require 1000 steps; the 8087 used microcode to specify these steps. The die photo above shows the “engine” that ran the microcode program; it is basically a simple CPU. Next to it is the large ROM that holds the microcode.
The bottom half of the die holds the circuitry that processes floating-point numbers. A floating-point number consists of a fraction (also called significand or mantissa), an exponent, and a sign bit. (For a base-10 analogy, in the number 6.02×1023, 6.02 is the fraction and 23 is the exponent.) The chip has separate circuitry to process the fraction and the exponent in parallel. The fraction processing circuitry supports 67-bit values, a 64-bit fraction with three extra bits for accuracy. From left to right, the fraction circuitry consists of a constant ROM, a shifter, adder/subtracters, and the register stack. The constant ROM (highlighted in green) is the subject of this post.
The 8087 operated as a co-processor with the 8086 processor. When the 8086 encountered a special floating-point instruction, the processor ignored it and let the 8087 execute the instruction in parallel.1 I won’t explain in detail how the 8087 works internally, but as an overview, floating-point operations are implemented using integer adds/subtracts and shifts. To add or subtract two floating-point numbers, the 8087 shifts the numbers until the binary points (i.e. the decimal points but in binary) line up, and then adds or subtracts the fraction. Multiplication, division, and square root are performed through repeated shifts and adds or subtracts. Transcendental operations (tan, arctan, log, power) use CORDIC algorithms, which use shifts and adds of special constants for efficient computation.”
