Other

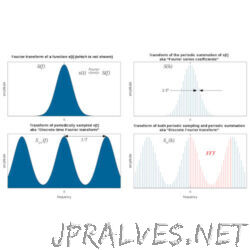
“The DFT provides an efficient way to calculate the time-domain convolution of two signals. One of the most important applications of the Discrete Fourier Transform (DFT) is calculating the time-domain convolution of signals. This can be achieved by multiplying the …

“More than a year ago, a friend of mine asked me to write the software for his 3D Spectrum Analyser (3DSA): a device that takes as input an audio signal, and outputs its visualisation on a 3D matrix of leds …